论文题目： The Fu？ík spectrum of Schr？dinger operator and the existence of four solutions of Schr？dinger equations with jumping nonlinearities 

　　论文作者：Chong Li(李翀)  Shujie Li(李树杰) 

　　问题背景：跳跃非线性问题源于等离子体物理(plasma)，生物捕食模型(Predator-prey model)和悬桥(suspension bridge)问题，而非线性Schr？dinger方程揭示了微观物理世界物质运动的基本规律，在非线性光学领域具有广泛应用。 

　　成果介绍：我们在Journal of Differential Equations(Volume263, Issue10, 2017, 7000-7097)发表了近百页的文章，率先系统研究Schr？dinger算子Fu？ík谱和相应跳跃非线性方程第四个非平凡解存在性，所面临的主要困难是紧嵌入缺失和本质谱出现，二者使得这一问题研究变得极具挑战性。我们要利用Morse不等式证明第四个解存在性，必须首先验证跳跃非线性方程对应泛函在适当假设下满足Palais-Smale条件，这一目标主要通过建立在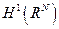上的Minimax原理实现，其次，已有方法只能得到三个解，一个正解，一个负解，一个变号解，要获得第四个解必须对正负解性质做出精确描述和刻划，即证明正负解是方程对应能量泛函的山路型临界点并完整算出山路型临界点临界群，这一目标主要通过我们建立在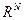上的弱极大值原理以及建立的新型splitting定理和shifting定理实现，此外，由于Morse不等式的整体性质是通过泛函在无穷远临界群来体现，而这与Schr？dinger算子Fu？ík谱线密切相关，基于此，在这篇文章中我们通过利用复杂的分析技巧对Schr？dinger算子Fu？ík谱线进行系统研究。有了上述准备工作，结合Morse不等式和一系列正合同调序列讨论，我们最终得到第四个解。 

　　论文地址： 

　　https://www.sciencedirect.com/science/article/pii/S0022039617303935