布尔方程系统求解问题是算法设计中的核心问题。判定其是否有解是NPC问题,而求解布尔方程系统则是NP问题。该问题涉及到量子算法核心问题，即NPC问题的多项式时间量子算法是否存在？该问题也是密码学研究的核心问题：它是流密码、分组密码、Hash函数等主流密码体系主要分析方法，也是抗量子计算候选密码多变量公钥密码(MPKC)的数学基础。 

　　本工作给出了布尔多项式系统求解的第一个量子算法，其复杂度关于方程大小和方程的条件数是多项式的，从而实现了对条件数小的稀疏布尔方程系统指数级加速。 

　　这一算法揭示了主流密码的抗量子计算攻击属性。非对称密码的三类主流密码体系包括AES，Trivium和SHA3/Keccak. 其中AES是分组密码国际标准(2001)，已经广泛使用；Trivium是流密码国际标准；SHA3/Keccak是新一代Hass函数国际标准。这些密码的破解都可以归结为非线性布尔方程的求解问题。应用本工作提出的布尔方程求解量子算法于以上主流密码的抗量子计算攻击分析，揭示了基于方程求解的密码体系的抗量子计算攻击属性：基于方程求解的密码体系只有在其条件数非常大时才可以抵抗量子计算攻击，进而揭示了对应方程的条件数是设计抗量子计算攻击密码的主要标准之一。 

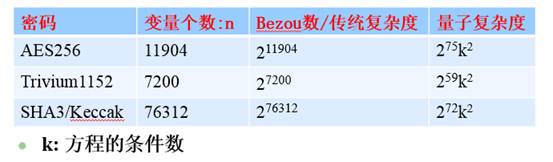
　　表1.主流密码体系的抗量子计算攻击属性 

　　与本成果相关的论文： 

　　1. Y.A. Chen and X.S. Gao, Quantum Algorithms for Boolean Equation Solving and Quantum Algebraic Attack on Cryptosystems, arXiv 1712.06239, 2017.