伊藤过程分解的唯一性是随机分析最基本的结论之一，有着广泛且重要的应用。特别地，它是概率方法研究偏微分方程的基础。为了用概率方法研究PDE，首先要在概率空间中刻画函数的导数。对于线性PDE，这等价于证明伊藤过程分解的唯一性，而对于非线性PDE，这等价于证明非线性期望下伊藤过程分解的唯一性。 

　　非线性期望下伊藤过程分解的唯一性是非线性期望领域多年未解决的一个公开问题。这也是Peng and Song (2015)中的遗留问题。该问题的难点在于如何区分三类形式不同，但均可能具有绝对连续路径的有限变差过程，因此传统方法不能处理这类问题。   

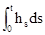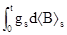　　我们严格区分了非线性期望下的三类有限变差过程（1.有限变差鞅，2.,3. ），证明了非线性期望下伊藤过程分解的唯一性. 

　　两位审稿人对我们的结果和证明方法给出了积极评价： 

　　Reviewer 1: 

　　“In this paper the author has solved a deep and fundamental problem in the framework of stochastic analysis with G-Brownian motion B.” 

　　“But as consequence, the above basic distinguishability problem becomes a challenging problem.” 

　　“Some of the results and techniques introduced in this paper are also very original and useful for further research in this domain.” 

　　“I think this paper contains excellent and original results and thus is publishable in this journal.” 

　　Reviewer 2: 

　　“The obtained result is an important breakthrough, not only for the theory of stochastic analysis under G-expectation.” 

　　“Let us emphasise that the proof of the main result, that of the uniqueness explained above, is rather tricky and technical, and full of new ideas. I like it very much.” 

　　“For this reason there is no doubt for me that the submitted manuscript merits to be published.” 

　　发表论文　　  

　　1. Song, Y. (2018): Properties of G-martingales with finite variation and the application to Sobolev spaces. Stochastic Processes and Their Applications. Available online at www.sciencedirect.com.