在薄壳的建模理论中，薄壳中面应力张量方程具有基础的重要性，例如，在薄壳分层理论中，当薄壳厚度趋于零时，薄壳非线性三维弹性能的Gamma极限（二维弹性能）就与薄壳中面的应力张量方程密切相关。此外，在薄壳的几何硬度理论中，薄壳中面的应力张量方程也起着决定性作用。 

　　然而薄壳中面应力张量方程的性质取决于薄壳中面的Gauss曲率。对正Gauss曲率或零Gauss曲率的薄壳中面，已有一系列结果。但对负Gauss曲率的情况，薄壳中面的应力张量方程研究十分困难。我院姚鹏飞最近58页的文章《Linear Strain Tensors on Hyperbolic Surfaces and Asymptotic Theories for Thin Shells》给出了负Gauss曲率情况下，薄壳中面应力张量方程可解性，解的正则性以及光滑解的稠密性等一系列结果。特别地，将这些结果应用于薄壳的分层理论，在分层能量级为 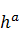（a在2与4之间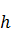，为薄壳厚度）时，对负Gauss曲率的中面，求得了薄壳非线性三维弹性能的Gamma极限--二维弹性能公式。 

　　该文章被SIAM Math. Anal. 接受。