矩阵优化是一类变量含有矩阵的优化问题。矩阵优化的研究是从半正定规划 (semidefinite programming)这一特殊矩阵优化问题开始的。半正定规划被认为是自上世纪五十年代的线性规划(linear programming)后，数学优化领域的突破性的进展之一。随着实际应用的不断发展，特别是大数据科学研究的兴起，过去二十多年，在统计、数据挖掘、机器学习、图像和信号处理、金融工程、信息学等领域的许多应用中，出现了越来越多的变量为（对称/非对称）矩阵的优化问题。一般矩阵优化逐渐成为数学优化研究的热点问题之一。 

　　优化问题的扰动分析作为数学优化理论研究中的一个重要本质问题，就是研究优化问题的解（最优解或者稳定点）随扰动变量改变的变化规律。除了其重要的数学理论意义，优化问题的扰动分析理论也为设计求解大规模矩阵优化问题高效算法、分析算法收敛性提供理论保障。在过去的三十年，包括INFORMS前主席S.M. Robinson（Dantzig奖），A.L. Dontchev，R.T. Rockafellar（Dantzig奖与von Neumann理论奖），B.S. Mordukhovich (AMS Fellow和SIAM Fellow), J.S. Pang（Dantzig奖），A. Shapiro（Dantzig奖）等许多知名优化与变分分析学者，都在优化问题扰动性分析方面展开了深入研究并取得了许多重成果。时至今日，对经典的非线性规划相关扰动性分析理论研究目前已经比较完备了。然而，对于一般矩阵优化问题，由于其本身的非多面体性，使得基于多面体变分分析的经典扰动理论变得不再适用。丁超与合作者在深入研究非多面体函数变分分析性质的基础上，在矩阵优化问题扰动性分析方面取得了若干创新性的成果。  

　　(1) 矩阵优化问题KKT解集映射的鲁棒孤立平稳性  

　　针对非线性含非多面体二阶可约锥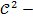（ reducible cone）的矩阵优化问题（包含非线性半正定规划问题），丁超与合作者证明了该性质等价与优化问题的二阶最优性条件和严格Robinson约束品性同时成立。这是第一次对于一般矩阵优化问题解集鲁棒孤立平稳性给出了其KKT解映射的鲁棒孤立平稳性的完整数学刻画。相关工作发表于优化顶级期刊SIAM Journal on Optimization。  

　　(2) 一类凸矩阵优化问题最优解集映射的平稳性  

　　丁超与合作者针对一般凸矩阵优化问题，给出了最优解集映射平稳性可验证的充分性条件，在此基础上证明了增广拉格朗日法求解凸矩阵优化问题时具有M.J.D. Powell教授（英国皇家学会会士）提出的局部任意阶快速线性收敛率。相关结果发表于优化顶级期刊SIAM Journal on Optimization。 

　　丁超与合作者在矩阵优化问题扰动性分析方面取得的成果得到了相关领域专家学者的关注。例如国际知名优化和变分分析专家B.S. Mordukhovich教授 (AMS Fellow和SIAM Fellow) 特别评论关于鲁棒孤立平稳性相关工作认为是一个突破性的结果并认为相应结果和采用的创新方法为将来其他重要研究开启了一扇大门 “This is a very strong paper, which contains breakthrough results in studying robust stability notions for non-polyhedral conic optimization problems… The results obtained and the methods developed open the gate for further important investigations”。这些结果不仅丰富了现有非多面体优化问题扰动分析理论，也为设计求解大规模矩阵优化算法提供了理论支撑。例如，关于凸矩阵优化集映射平稳性以及增广拉格朗日法收敛性结果，为基于半光滑牛顿法的求解半正定规划算法包SDPNAL/SDPNAL+（2018 年度Beale-Orchard-Hays 计算奖） 的有效性提供了理论保证。   

　　相关论文：