
迄今为止,有界障碍反散射问题的理论与算法已得到非常广泛而系统的研究(Colton-Kress, 2013)。然而在诸如地质勘探、地震学、卫星遥感和无损探测等重要的实际应用中,往往还会遇到一类非常重要的反散射问题,即无界粗糙曲面反散射问题(对于散射模型的描述,参见图1和图2)。对于此类反散射问题,散射场不再满足通常的 Sommerfield 辐射条件,而是满足更为复杂的向上传播辐射条件(UPRC条件)。此外,由于测量条件的局限性,通常只能在上半空间获取有限孔径(limited aperture)的测量数据,这使得反散射问题的不适定性大大增加。进一步地,由于粗糙曲面的无界性,很多已有的反问题算法不再适用。因此,无界粗糙曲面反散射问题是一个非常具有挑战性的课题。
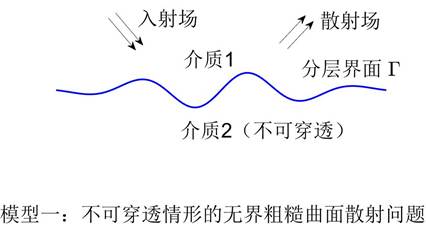
图1
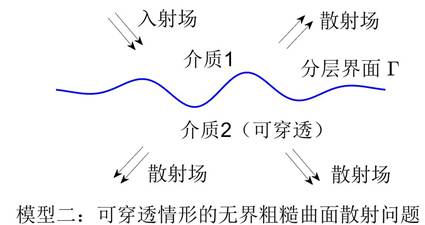
图2
与张波研究员和刘晓莉博士合作,我们提出了利用点源入射产生的声波散射近场柯西(Cauchy)数据重构无界粗糙曲面的直接成像算法,并利用散射解的渐近性质和交互关系(reciprocity relation)给出了算法的理论分析。该方法对噪音的敏感性小,并且对于可穿透和不可穿透曲面都能得到很好的重构结果。进一步地,与他人合作,我们将该工作推广到了更为复杂的弹性波反散射情形。相关工作见论文[1, 2, 3]。
与张波研究员和徐小绪博士合作,我们研究了相位缺失近场数据情形下声软局部粗糙曲面反散射问题。证明了可数个平面波入射产生的无相位近场数据能够唯一确定未知边界。基于此,借助于震荡积分理论(特别是稳定相位方法),提出了利用无相位近场数据快速重构局部粗糙曲面的直接成像算法。相关工作见论文[4]。
论文列表:
[1] Xiaoli Liu, Bo Zhang and Haiwen Zhang, A direct imaging method for inverse scattering by unbounded rough surfaces, SIAM Journal on Imaging Sciences 11 (2018), 1629-1650.
[2] Guanghui Hu, Xiaoli Liu, Bo Zhang and Haiwen Zhang, A non-iterative approach to inverse elastic scattering by unbounded rigid rough surfaces, Inverse Problems 35 (2019), 025007.
[3] Xiaoli Liu, Bo Zhang and Haiwen Zhang, Near-field imaging of an unbounded elastic rough surface with a direct imaging method, SIAM Journal on Applied Mathematics 79 (2019), 153-176.
[4] Xiaoxu Xu, Bo Zhang and Haiwen Zhang, Uniqueness and direct imaging method for inverse scattering by locally rough surfaces with phaseless near-field data, SIAM Journal on Imaging Sciences 12 (2019), 119-152.
附件下载: