有限元方法是数值求解偏微分方程的最有力的工具之一，已经广泛得到成功应用，作为一门响应实际驱动而具有非常强的理论性的方法论学科获得了长足的发展。在已有的研究基础上，如何做到更好的与实际计算条件相匹配、与并非专研有限元的用户的知识背景相结合、以及如何充分发挥多年研究积累起来的丰富的算法、理论和软件成果的积极作用，都是对有限元方法的设计和分析提出的自然的要求。作为从二阶椭圆问题向高阶问题和更复杂问题过渡的中间承启，四阶椭圆问题有限元方法的研究比较集中地体现了这些方面的要求。 

　　四阶椭圆问题指不高于四阶而可以导出二阶 Sobolev 空间上的椭圆型双线性形式的微分方程，是数学和应用科学中一类重要的模型问题，内涵丰富、应用广泛，其有限元方法研究具有重要意义，相应地，在贴近实际弱化条件发展算法、总结定性特征并指导有针对性的算法设计等方面都面临更大的难度，有很多基本问题还没有解决。同时，四阶算子常常在形式上表现为二阶算子的组合，从而二阶问题的研究经验看起来应该在四阶问题的研究中发挥更大作用; 这是一个很自然的要求，但如何设计算法并在理论上给以保证，实际上仍很有研究空间。 

　　在这样的启发和驱动下，张硕在四阶问题相关领域开展有限元基础算法和理论研究，完成了一些工作。 　　  

　　1 无结构网格双调和方程有限元系统最优求解器设计  

　　用有限元格式离散微分方程产生大规模线性代数方程组，其求解是有限元方法求解微分方程全过程中最耗费时间和计算资源的步骤，为其设计最优求解算法是计算数学的一个基本问题。元形式 (primal formulation) 的双调和方程模拟板的最小势能原理，从实际应用的条件出发，在不假设网格具有分层结构的应用条件下设计双调和方程有限元系统的最优求解器具有明确的理论意义和应用价值；同时，这个问题的研究尚少见相关结果，具有一定的挑战性。  　　  

　　张硕和合作者提出了一套算法([张硕-Xu: SINUM2014]), 用于求解离散双调和方程的各类边值问题所得到的有限元线性系统, 在不假设网格具有分层结构的条件下，严格证明了这套算法的计算复杂度是最优的，从而在文献中首次证明了无结构网格上双调和方程有限元系统可以最优求解。这套算法适用于所知的各种协调元和非协调元针对多边形区域导出的系统，特别地，不依赖于理论分析中一般用到的标准的区域凸性假设。这套方法的主要的要素是，精准配置 Poisson 方程有限元系统求解器而设计了形式统一、计算代价最优的最优预条件子; 事实上，预处理之后的系统可能含有若干个渐进无界的特征值，通过数学上的分析，这些无界特征值的数目得到了严格刻画，它是固定有限的、极小且与问题规模无关，从而这几个无界特征值的可能存在不影响整个算法的计算效率。此外，因为主要的工作量以求解 Poisson 方程的形式进行，这套算法可以很自然地与通用的软件包和种类丰富的 Poisson 方程求解器对接。  　　  

　　2 双调和方程低次丰满有限元格式设计  

　　求解双调和方程的有限元格式，如果所采用分片多项式的总次数不高于 k 次而误差的能量模的收敛速度达到 O(hk？1) 量级, 则称此有限元格式是丰满的(optimal)。丰满格式的收敛速度和其使用的分片多项式空间互相对应地达到了理论上界和下界，是不可改进的，具有鲜明的临界特征。精度的丰满与否是刻画有限元格式的重要的定性特征，也易为其它知识背景的研究者所理解和接受，具有基本的理论意义，然而，一些看起来很简单的情形下，其设计问题仍未获得解决。例如，图1展示了正方形区域两种最典型网格。de Boor-DeVore-Hoellig 证明，在图左类网格上，三次连续可微有限元格式求解双调和方程必然会丢失一阶精度，三次丰满格式即付之阙如; 图右正方形网格上，求解双调和方程(甚至 Poisson 方程)的二次丰满格式亦无人知。这样的状况让人多少有些意外，也说明丰满有限元格式的研究仍有比较基本的意义和较大的空间。  

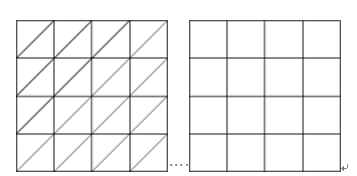
　　图 1. 两类基本网格示意图.  

　　张硕提出了一种四边形网格上的非协调有限元格式([张硕: IMANA])，该格式采用分片二次多项式离散双调和方程，在标准的光滑性假设下具有一阶能量模精度，从而是丰满的。这是双调和方程丰满有限元格式在四边形网格甚至正方形网格上所知的第一个结果，是理论上的最低次结果。该非协调元格式采用类似样条有限元的方式来定义，标准的基于节点插值算子的误差分析技巧无法生效。作者为此设计了将逼近性误差转化为辅助有限元问题离散误差的分析方法，对相关科学问题给出了正面的回答。上述辅助有限元问题是借助前期工作 [张硕: NM2016] 中提出的四边形网格上的有限元 Stokes 复形来构造的。有限元复形是主要由 Arnold 等人倡导发展起来的有限元外计算理论的基本研究对象，是过去二十年的研究热点。此文的结果是所知的第一个在一般四边形网格上成立的多项式有限元复形。类似的研究方法可以推广到在形状规则的任意三角形网格上(含图1三角形网格)构造双调和方程三次丰满有限元格式。  　　  

　　3  一般四阶椭圆型问题降阶格式构造  

　　降阶格式(包括传统上称为混合元的格式)会给四阶问题计算带来一些方便; 例如，降阶格式只需要离散一阶 Sobolev 空间，从而有限元空间较容易保有嵌套性质，张硕及其合作者利用此性质设计了基于降阶格式的四阶特征值问题的最优多重网格方法，并针对若干模型问题取得了成功实践，相关文章已经发表于J. Sci. Comput. 及 IMA J. Numer. Anal.。降阶格式还可以充分利用二阶问题的大量算法、理论、代码和软件产品，对于用户更加友好。考虑到一事一议地设计基于元形式的有限元格式的难度，在“一般四阶问题”的设定下发展构造降阶格式的统一方法既有助于打好与不断涌现的新的四阶问题的“遭遇战”，也具有非常具体的实际意义。  

　　四阶问题降阶格式方面已经有一些工作。以双调和方程为例，常见的使用困难有：降阶形式与元形式的等价性一般依赖于额外的正则性假设、其稳定性结果一般建立在负阶次 Sobolev 空间上、而且这些降阶格式一般假设源项具有 H？1 及以上正则性而不讨论源项仅有 H？2 正则性的情形。这些特点都需要用户在使用时多加小心。对于其它四阶问题来说，基于同样思路的降阶格式也会遇到类似的情况。  

　　张硕研究了一般四阶问题降阶有限元格式的构造问题([张硕: NM2018])，构造了建立在一阶空间组合上的稳定的变分方程组, 实现无条件等价的降阶处理；在此基础上提出了渐进保结构的离散格式的统一框架。该设计框架克服了上面提到的常见困难，是对一般的四阶问题有效的，已经于若干常见和新近研究较多的四阶问题上得到验证。  

　　这种方法框架的基础是空间的稳定求和理论(及相应的结构性稳定分解理论)，这种基于空间结构的构造理念已经在若干问题上表现出生命力。例如，[张硕: M2AN2018]基于空间结构性分解设计了四重旋度方程的解耦格式，这是该问题首个无需额外正则性假设即可证明与元形式等价的降阶格式; 同时，借助于该形式，申请人建立了模型问题的正则性估计，确认了先前发表于 Mathematics of Computation 、Numerische Mathematik等刊物的一些工作中作为误差分析和格式等价性基础的正则性假设的有效性。　　  

　　代表性论文 　　  

　　[张硕-Xu: SINUM2014] Z. & Jinchao Xu: Optimal solvers for fourth-order PDEs discretized on unstructured grids, SIAM Journal on Numerical Analysis, 52(2014), 282–307. 　　  

　　[张硕: NM2016] Z.: Stable finite element pair for Stokes problem and discrete Stokes complex on quadrilateral grids, Numerische Mathematik 133(2016), 371–408.  　　  

　　[张硕: M2AN2018] Z.: Mixed schemes for quad-curl equations, ESAIM: Mathematical Modelling and Numerical Analysis, 52(2018) 147–161.　　  

　　[张硕: NM2018] Z.: Regular decomposition and a framework of order reduced methods for fourth-order problems, Numerische Mathematik, 138(2018), 241-271.　　  

　　[张硕: IMANA] Z.: Minimal consistent finite element space for the biharmonic equation on quadrilateral grids, IMA Journal of Numerical Analysis, 已在线发表. Doi: 10.1093/imanum/dry096.