SD猜想是Clay数学研究所在2000年提出的七大千禧年数学难题之一。指出了椭圆曲线的Mordell-Weil 群和它的L-函数的关系。BSD猜想分为秩部分和公式部分。BSD猜想的秩部分可以陈述为： 

　　其中的3)到1)就是“椭圆曲线上的p-逆定理”。 　　  

　　张伟, C.Skinner分别在2013年证明了无复乘情形的椭圆曲线上的p-逆定理。本工作证明了带复乘情形椭圆曲线上的p-逆定理。具体介绍如下。   

　　假设E是定义在有理数域上的带复乘的椭圆曲线且p>3是素数满足E在p处有好的正常约化, 我们证明了若E的p-Selmer 秩为1则其L-函数在中心处的解析秩也为1.即.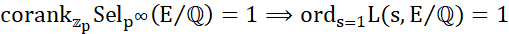 

　　这一成果的创新之处在于我们构造了在复乘域上的自对偶且L-函数的符号为-1的Rankin-Selberg对 （其中的模形式有非平凡的中心特征），并利用复乘的主猜想及rigid原理来建立了相关情形下的Perrin-Riou Heegner点主猜想。 

Burungale, Ashay A.,Tian, Ye p-converse to a theorem of Gross-Zagier, Kolyvagin and Rubin. Invent. Math. 220 (2020), no. 1, 211–253.