机械臂是目前应用最广的工业机器人。冗余机械臂是一类更加灵活、更适用于人机合作的工业机械臂，其运动学反问题与奇异性是机器人控制过程中的基础问题。数学机械化实验室李子佳副研究员与奥地利乔安娜研究所的Hofbaur教授等人合作，给出了一类冗余机械臂的运动学反问题的闭形式解。他们利用Gr？bner基等工具给出了详尽的机械臂运动奇异性分析。相关工作被机器人顶级期刊IEEE Transactions on Robotics发表，并受邀于2023年机器人技术领域最有影响力的国际学术会议IEEE International Conference on Robotics and Automation做全文报告。 

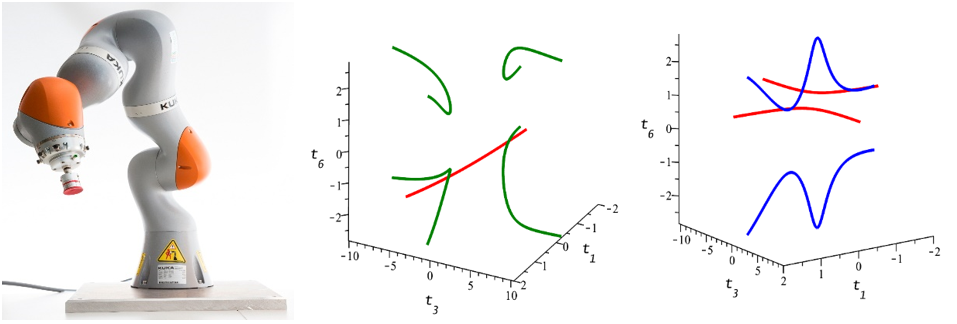
　　李子佳等人的最新工作完整地给出了一类7轴机械臂的运动学反问题的闭形式解，以及闭形式解间之间的代数关系，并将其推广至2n+1轴情形。特别地，他们在利用Gr？bner基求解其运动奇异性过程中，首次发现该7轴机械臂的一种运动奇异性与避障的运动矛盾，该奇异性是由机械臂的特定机构设计所导致的；他们发现2n+1轴的运动学奇异性的代数约束都有可能被素分解成为线性的，并验证了n=5,6,7的情形。

　　参考文献：  

　　Zijia Li, Mathias Brandst？tter, Michael Hofbaur. Kinematic Redundancy Analysis for (2n+1)R Circular Manipulators. IEEE Transactions on Robotics, 2022 online, 1-13.