
由于“维数灾难”的原因,求解高维偏微分方程一直是数学、物理、化学等学科中具有本质困难的问题。基于深度神经网络的机器学习方法为解决这一问题提供了潜在的可能性,目前已经设计了多种机器学习方法来求解高维偏微分方程。这些方法由于需要进行采样或使用Monte-Carlo方法进行高维积分来计算损失函数,往往导致求解精度远低于经典算法求解低维偏微分方程的精度,实际应用范围也受到了很大的限制。
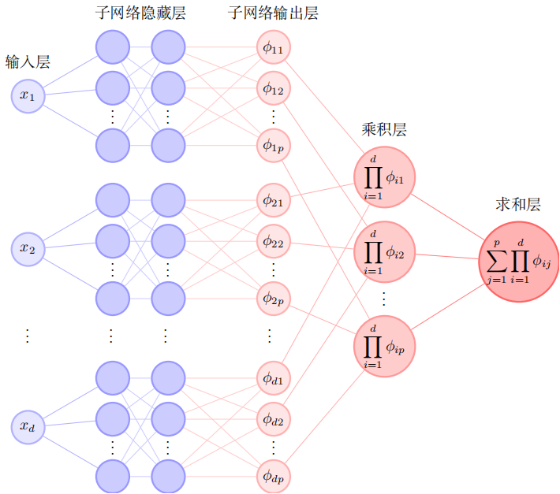
为了提升机器学习算法求解高维偏微分方程的精度,谢和虎课题组提出了张量神经网络(TNN)结构及其相应的机器学习算法。张量神经网络最重要的特点是可以将损失函数中高维积分的计算转化成一维积分的计算,从而可使用经典的数值积分格式得到高精度的高维积分,进而使得相应的机器学习方法的精度远超其它类型的机器学习方法。
课题组的研究生利用基于张量神经网络的机器学习方法参加了2023年“大湾区”粤港澳AI for Science科技竞赛,在求解高维偏微分方程竞赛中得到了最好的精度,并获得了大赛的特等奖。
该方法被国内外多个课题组用于高维偏微分方程求解,包括PINN的提出者Karniadakis教授及其课题组用于高精度求解20,000维包含耦合势能的Schrodinger方程和高维的Fokker-Planck方程。

相关论文:
1. Yifan Wang, Pengzhan Jin and Hehu Xie, Tensor neural network and its numerical integration, Journal of Computational Mathematics, doi:10.4208/jcm.2307-m2022-0233, Journal of Computational Mathematics JCM (global-sci.org)
2. Yifan Wang and Hehu Xie, Computing multi-eigenpairs of high-dimensional eigenvalue problems using tensor neural networks, Journal of Computational Physics,506 (2024), 112928.
3. Yifan Wang, Zhongshuo Lin, Yangfei Liao, Haochen Liu and Hehu Xie, Solving high dimensional partial differential equations using tensor neural network and a posteriori error estimators, arXiv:2311.02732V2, 2023.
中国科学院国家数学与交叉科学中心
2024年6月26日
附件下载: