几何引擎是设计研发类工业软件CAD（计算机辅助设计）系统的“心脏”和“发动机”，CAD中曲面的自交现象对几何引擎中求交、网格化、渲染等核心功能的计算稳定性造成极大干扰。适用于CAD几何引擎的NURBS曲面自交快速判定和计算是CAD领域长期以来的困难问题。

近日，数学机械化实验室贾晓红研究员、李凯博士与中国科学技术大学陈发来教授合作攻克了该问题，提出曲面自交的代数判别式和自交轨迹的快速保拓扑计算方法，NURBS曲面自交判定平均效率达到10^-4秒级，并在挑战性临界拓扑的计算正确性上优于商业引擎ACIS。相关成果被计算机图形学顶级期刊ACM Transactions on Graphics接收发表。

曲面的自交线由曲面上的奇点组成，曲线曲面的奇点理论是代数几何和计算几何的共同研究对象，奇点的快速稳定计算也是计算几何领域的挑战性问题。在计算代数几何理论中，有理曲线曲面的奇点可通过Groebner基或结式法进行分析。 对于奇点的快速计算，历史上的个别相关符号算法均未给出奇点的自然参数、难以计算尖点及孤立奇点、不能计算奇点的阶数、容易产生冗余结果、在曲面参数化具有复杂基点时失效，并且往往难以数值化。

在过去二十年间，在奇点计算的基础理论和应用方面，贾晓红及其合作者曾依次证明了平面有理曲线奇点稳定计算的猜想、发展了空间有理曲线的奇点分类理论和算法、解决了计算几何领域在有理曲面奇点计算的公开问题。本工作是有理曲面奇点计算理论向CAD工业软件领域的进一步拓展。

2008年，中国科大陈发来与香港大学王文平等提出用动直线理论解决平面有理曲线奇点快速稳定计算的方法，并提出动直线矩阵完整给出曲线奇点解消结构的猜想[Chen, Wang and Liu, Journal of Symbolic Computation, 2008]。贾晓红与莱斯大学Ron Goldman教授于2012年完成了该猜想的证明[Jia and Goldman, Computer Aided Geometric Design, 2012]。

然而，动平面理论是否可类似地应用于曲面的奇点计算？该问题被代数几何学家、美国数学会会士David Cox等提出，并在2016年国际计算代数与几何建模大会（CAGM2016）被三位大会主席（Laurent Buse、Ron Goldman、Hal Schenck）在大会综述中特别指出“仍是公开问题”。贾晓红与陈发来、姚姗姗于[Jia, Chen & Yao, ACM Transactions on Graphics, 2022]完整解决了该公开问题，利用动平面理论，证明了有理曲面的动平面簇与曲面奇点的参数、重数之间的内蕴联系，并给出一般有理曲面奇点的参数和阶数的快速稳定算法。

    以上理论和算法研究可以用于CAD领域的NURBS曲面自交计算。然而，几何引擎核心工业软件对自交判定效率有极高要求，通常要求在毫秒内完成计算，过去的理论和算法难以达到。近日，项目组基于CAD中NURBS曲面表示本身的特殊性，给出了NURBS曲面自交的快速判别式，仅通过曲面控制点的简单线性组合即可指示曲面是否自交，避免了传统的对复杂代数系统的求解，平均判定效率达到10^-4秒，同时也给出NURBS曲面自交线轨迹的快速计算算法。经与商业几何引擎ACIS、开源几何引擎OCCT的对标测试，该算法在自交线包含小环、奇点、斜接点等复杂拓扑情况下计算更为稳定[Li, Jia & Chen, ACM Transactions on Graphics, 2025]。

Publication: 

ACM Transactions on Graphics (Fast Determination and Computation of Self-intersections for NURBS Surfaces.2025)

Authors: 

K. Li

Academy of Mathematics and Systems Science, CAS, Beijing, China 

E-mail: likai@amss.ac.cn

X. Jia 

　 Academy of Mathematics and Systems Science, CAS, Beijing, China

   E-mail: xhjia@amss.ac.cn

F. Chen,

　 University of Science and Technology of China

   E-mail: chenfl@ustc.edu

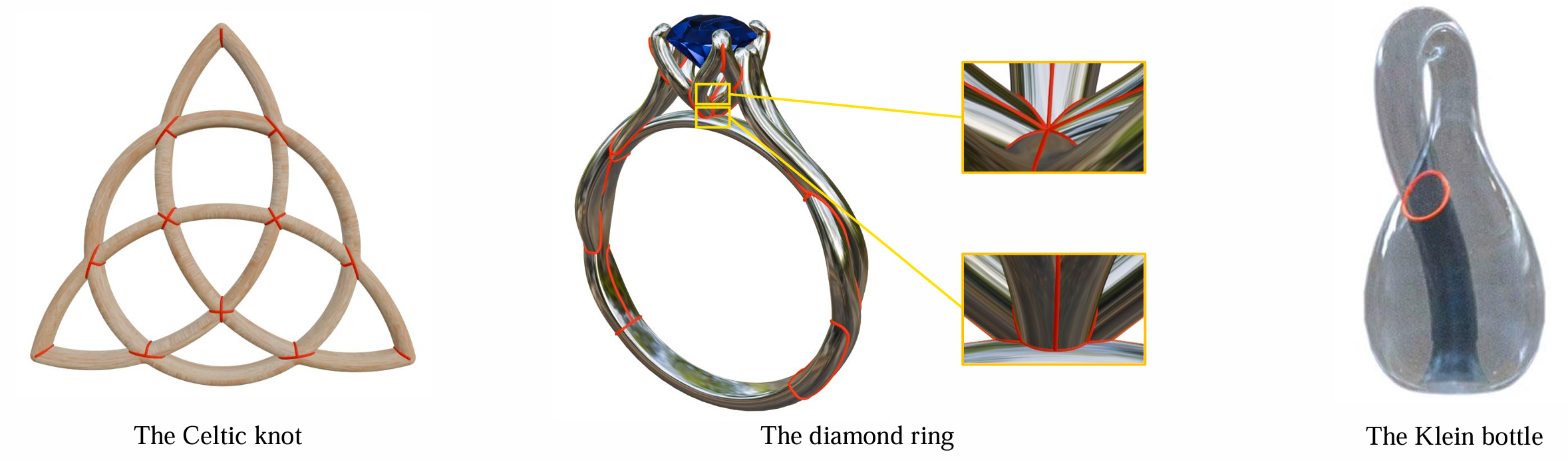
图表 1：CAD模型自交线计算

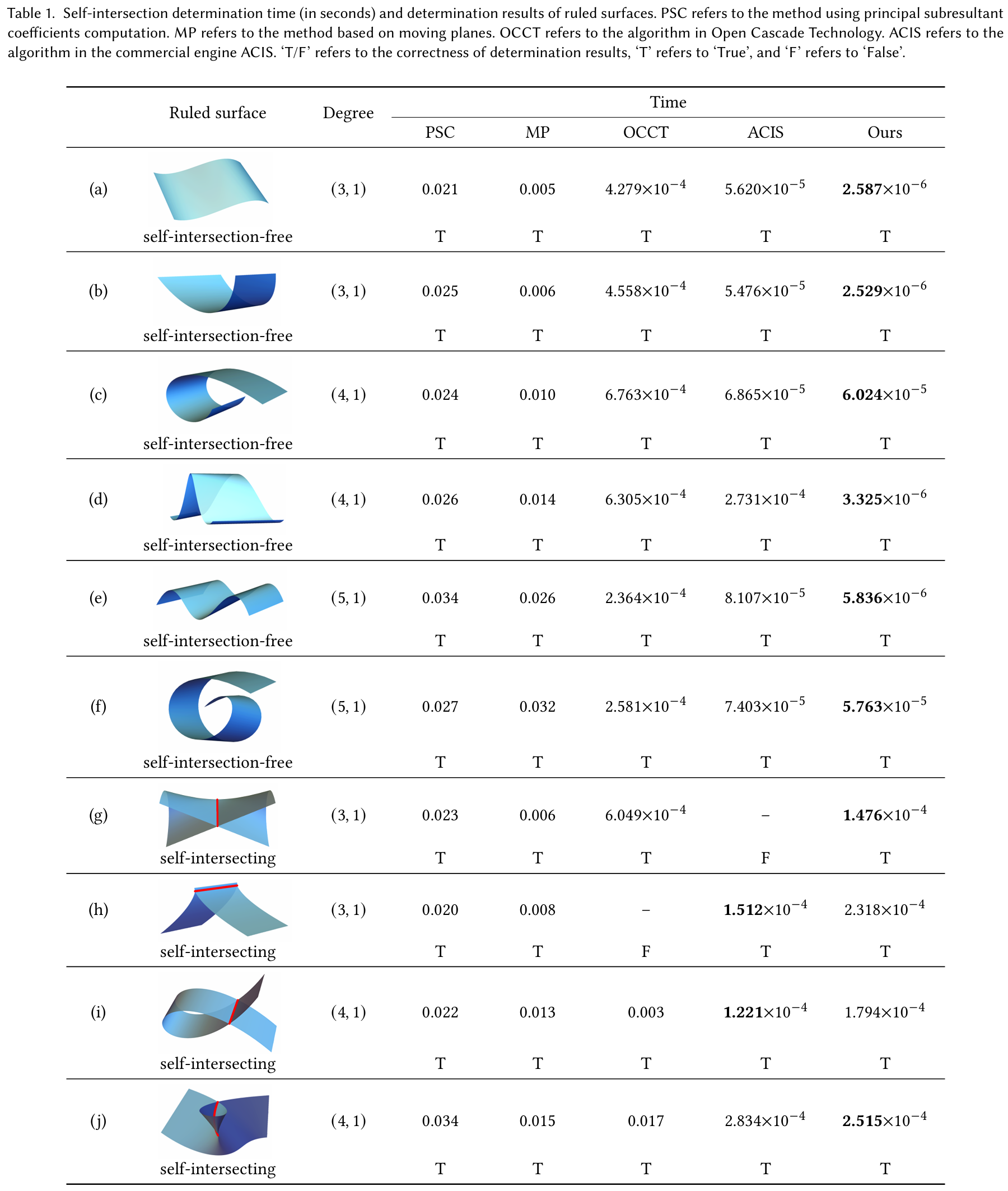
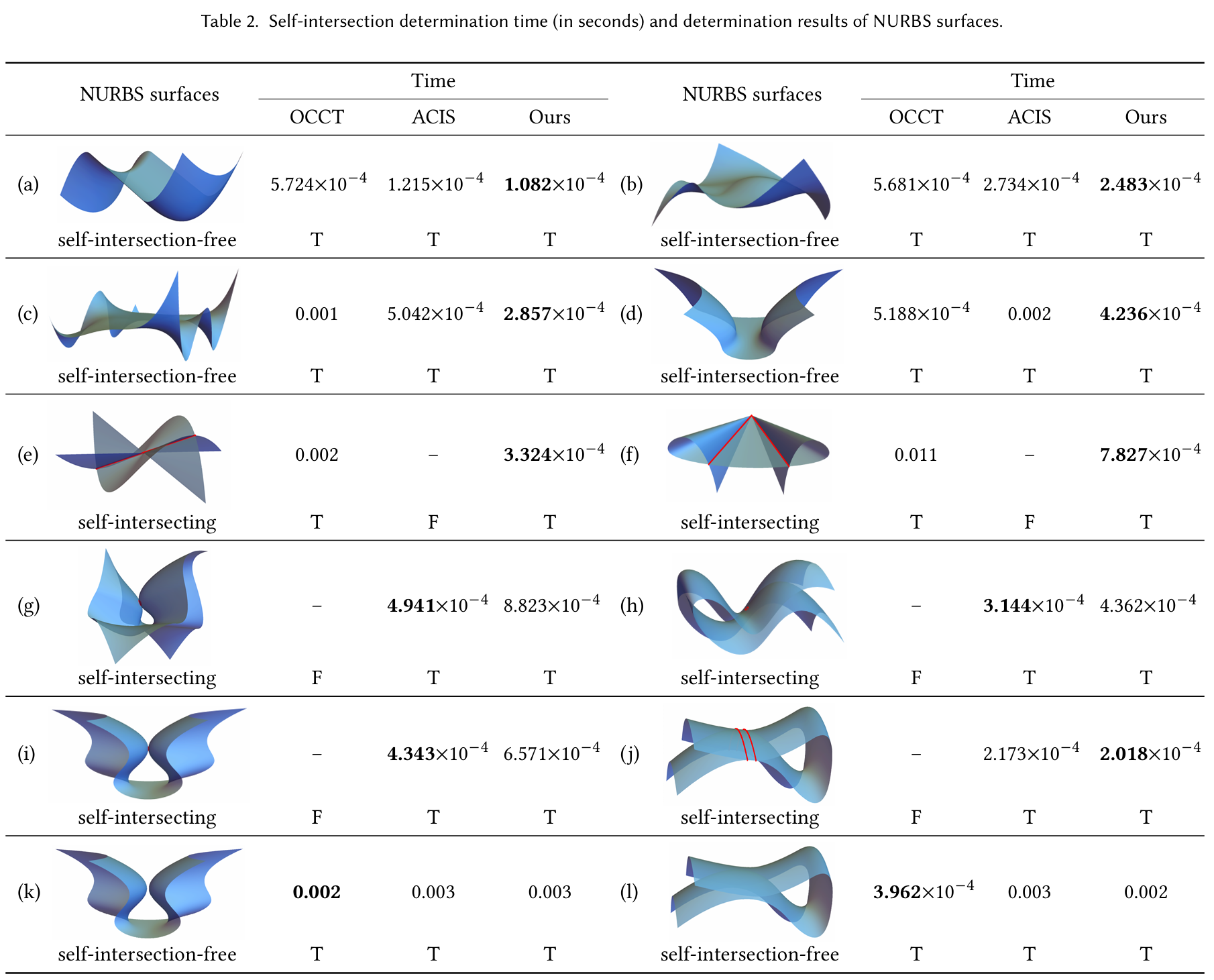
图表 2：NURBS曲面自交判定效率与其他几何引擎的对比