(尚云 陆汝钤)量子计算基础理论和量子点元胞自动机的器件设计优化
一.量子计算基础理论
1. 在新型量子通讯原理方面
我们通过引入两硬币量子游走模型首次将量子游走应用于量子通信协议中,分别提出了基于直线,圆,完备图和正则图上的量子隐形传输模型【1,2】;第一次将两硬币量子游走模型用于完美状态转移协议的设计,对比已存单硬币模型初次实现了高维态在一般图形上的最优状态转移协议【2】。提出的隐形传输理论框架已被印度学者在IBM Q量子计算机平台给出了量子模拟验证;而完美状态转移框架由尚云课题组在IBM Q量子平台给出了模拟和实验实现(基于超导芯片)【3】。
2. 在最优测量方面
<1> 彼此无偏基问题
非素数幂维数的Hilbert 空间含有多少个彼此无偏基(MUB)一直是一个公开问题。当前人们致力于寻找不同的方法来构造彼此无偏基, 以突 破 N(d) 现有的下界
(1) 对于两体系统,我们研究了两两无偏的极大纠缠基问题。利用高斯和的性质,对于 c^{d}*c^{kd} 系统,发现d 为素数的乘积且为奇数时,下界为2( p^{a}-1) , 提高了已有下界p^{a}-1【4】。
(2)对于单体系统,当阶为素数幂 (d = p^ a ) 时, 我们构造出彼此正交非凡超方((MOES)的完备集, 从而可得 MUB 的完备集. 我们定义了任意阶的 MOES ([Ghiu and Ghiu, 2014] 中的定义仅限于阶为素数幂). 对于任意阶d, 我们建立了 MOES 与 MUB 的关系,并构造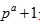 个MOES, 从而可得
个MOES, 从而可得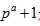 个 MUB【5】。
个 MUB【5】。
<2> 量子态的层析问题
我们研究秩为1的纯态信息真正完备的POVM测量,证明了Finkelstein的结果在维数d=2和4时确实是精确下界,而一般情况下Finkelstein给出的下界是不紧的,回答了Finkelstein提出的悬疑问题【6】。
3. 在开放系统量子计算理论方面
我们系统深入地研究了开放量子系统的量子可计算性,建立了第一个基于不分明量子逻辑的Chomsky计算体系(包括 0,1,2,3 型),发现并证明了该体系区别于经典计算体系和封闭量子计算体系的一系列特殊性质,揭示了量子计算原理在封闭系统和开放系统中有重大区别的根本物理原因;首次发现并证明了开放量子环境中量子图灵机的一系列不寻常性质,比如:确定型和非确定型量子图灵机不等价,不存在通用量子图灵机,量子图灵机的可计算能力超越了经典图灵机和欧洲科学院院士 Wiedermann 的模糊图灵机等。量子逻辑学家Peter Hines 在Math Review 评论说此项工作的“创新点是把图灵机和更加复杂的不分明量子逻辑结合起来,……,确实具有有趣的性质,和经典图灵机有着重要的相似点和不同点。”【7,8,9】
二.量子点元胞自动机的器件设计优化
我们首次突破了量子点元胞自动机电路的设计优化问题,给出了第一个择多门通用设计算法和最优化设计算法【10】。审稿人评价说“作者们在这个领域做出了很大的贡献。这在纳米终端是很少有人能够做到的。…这些结果将在最优化设计中非常的有用【10】。”该文目前Google Scholar 他引达 122次。
相关研究成果:
[1] Wang Y., Shang Y., Xue P. (2017), Generalized teleportation by quantum walks. Quantum information processing, 16, 221.
[2] Shang Y., Wang Y., Li M. and Lu R.Q. (2018), Quantum communication protocols by quantum walks with two coins. Europhysics Letters 124(6).
[3] Shang Y., Li M.(2019), Experimental implementation of state transfer by quantum walks with two coins, Quantum Science and Technology, 5(1),015005.
[4] Cheng X.Y. , Shang Y. (2018), New bounds of mutually unbiased maximally entangled bases in c^{d}*c^{kd}. Quantum Information and Computation ,13&14, 1152-1164
[5] Cheng X.Y.,Shang Y. (2018),Construction of orthogonal extraordinary supersquares and mutually unbiased bases. Science China:physics,mechanics & astronomy. 48(11),1-9.(In Chinese)
[6] Wang Y., Shang Y. (2018), Pure state‘really’informationally complete with rank-1 POVM. Quantum Information Processing, 17, 51.
[7] Shang Y., Lu X., Lu R.Q. (2012), A theory of computation based on unsharp quantum logic: finite state automata and pushdown automata. Theoretical Computer Science,434, 53-86.(SCI)
[8] Shang Y., Lu X, Lu R.Q. (2015), Computing power of Turing machines in the frame work of unsharp quantum logic. Theoretical computer science, 598, 2-14.
[9] Shang Y, Lu X, Lu R.Q. (2009), Automata theory based on unsharp quantum logic. Mathematical Structures in Computer Sciences,19,737-756.
[10] Kong K., Shang Y., Lu R. Q. (2010), An optimized majority logic synthesis methodology for Quantum-dot cellular automata. IEEE Transaction on Nanotechnology, 2010, 19, 170-183.